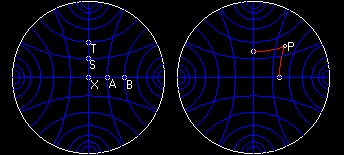
The
figure above shows 24 infinite lines which can be used to define a coordinate
system in Hyperbolic Geometry. Point X is at the origin of this coordinate
system. The horizontal and the vertical lines that intersect at the
origin are the x-axis and y-axis. In the figure, each the axis is
marked off by perpendicular lines that intersect the axis at intervals
of 0.5 units. For example, the length of segment XA = BC = AS = ST
= 0.5 units. In both Euclidean and Hyperbolic Geometry, we define
the coordinates of any point in the first quadrant to be the ordered
pair that is the perpendicular distance from the point to the x-axis, and
to the y-axis. In spite of the fact that we use the same definition
for coordinates in both geometeries, we cannot use the usual Euclidean
method of locating points in Hyperbolic Geometry. For example, in
Euclidean Geometry, to locate the point (1,1), we might first locate the
perpendicular to the x-axis that is one unit from the origin, then locate
the perpendicular to the y-axis that is one unit from the origin, and finally
locate the intersection of these perpendiculars. This procedure,
however, does not work in Hyperbolic Geometry. Notice that the perpendicular
to the x-axis that is one unit from the origin (at point B), and the perpendicular
to the y-axis that is one units from the origin (at point T), do not
intersect! This might make it seem like the point (1,1)
is undefined in Hyperbolic Geometry; however, the point (1,1) does exist,
and it is located at point P. The length of the perpendicular from
P to the x-axis is 1.0 units, yet the distance from the origin to the point
where the perpendicular crosses the x-axis is only 0.7 units.
This coordinate system sets up a one-to-one correspondence between all of the points in the first quadrant and all ordered pairs (x,y) where x and y are positive real numbers.
What does the equation: y=x² look like in Hyperbolic Geometry?
NonEuclid Home
Next Topic - Using NonEuclid - My First Triangle