Ideal points

The properties of incidence in the euclidean plane show a lack of symmetry,
for while two distinct points always define a line, two distinct lines
either define a point or are parallel.

To achieve symmetry, we introduce additional points, called ideal points for the plane.
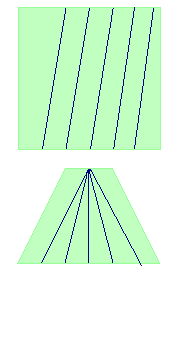
Note that these are purely abstractions, they do not correspond to points in a picture.
It may be useful to think of the plane viewed at an angle,
then the ideal line corresponds to the horizon.

Definitions
The ideal line for the euclidean plane E is the set {â : a is a direction in E}.
The elements of the set are the ideal points for E.
The extended plane Ê consists of E, together with the ideal points for E.

A direction in E may be defined by a line through O, or as a class of parallel lines.

We must now define lines and incidence in Ê.

Definitions
If L is a line on E, then the extended line, L⁺, consists of L, together with
the ideal point associated with the direction of L.
The lines of Ê are the ideal line and the extended lines L⁺ for L on E.

Incidence in Ê

Two points P, Q in Ê.
- P, Q on E. Then the points define a unique line L on E, and hence a unique line L⁺ on Ê.
- P on E, Q ideal. Let L be the line on E through P in the direction associated with Q.
  Then L⁺ is the only line on Ê containing both P and Q.
- P, Q ideal. Then the only line of Ê containing both is the ideal line.
Two lines L, N on Ê.
- L=K⁺, N=M⁺ for some K, M on E.
  If K and M are parallel, then L and N meet only in the ideal point for their common direction.
  Otherwise, K and M intersect at a point P of E. Then as L and N
  have different ideal points (directions), they meet only at P.
- L=K⁺, N is the ideal line. Then L has just one ideal point, so meets N only once.

Two points define a line

Two lines define a point

Geometry Page

Main Conics Page

Main Cabri Page