The Equal Angles Theorem

In inversive geometry, we shall generally regard angles as signed quantities. If OA and OB are segments, then there is a unique rotation about O taking A onto the ray OB. We regard this as defining the angle AOB (note the order of the letters). With this definition, we clearly have <BOA = -<AOB.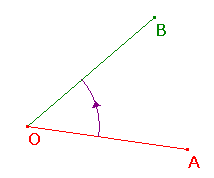
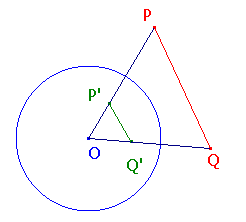
The Equal Angles Theorem Suppose that C is a circle with centre O, and that P and Q are points other than O. Let P and Q have inverses P' and Q' with respect to C. Then <QPO = <OQ'P' (in magnitude and sense) Proof Let r denote the radius of C. As P and P' are inverse, OP.OP' = r2. As Q and Q' are inverse, OQ.OQ' = r2. Thus, OP.OP' = OQ.OQ', so OP/OQ = OQ'/OP'. Hence, triangles OPQ and OQ'P' are similar. (Note the order of the vertices!) It follows that the given angles are equal in magnitude and sense.
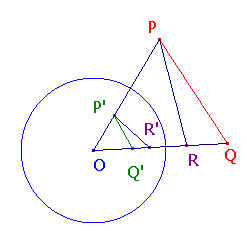
Corollary to the Equal Angles Theorem Suppose that P, Q and C are as in the theorem, and that R lies on the line OQ. Let R' be the inverse of R with respect to C. Then <QPR = <R'P'Q' (in magnitude and sense) Proof <QPR =<QPO - <RPO =<OQ'P' - <OR'P' by the Theorem =<R'P'Q' by the exterior angle property for triangle P'Q'R'

Main inversive page

Introduction to Conics

Introduction to Cabri

My Home Page