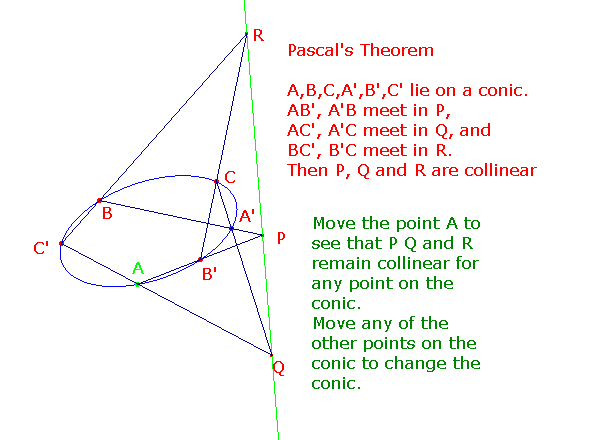
Note that, if we take the points A,B',C,A',B,C' (in that order) as the vertices of a hexagon, then the line pairs (AB', A'B, etc) are pairs of opposite sides of the hexagon.

Thus the theorem can be stated as
If the vertices of a hexagon lie on a conic, then the intersections of opposite sides are collinear.
See Brianchon's Theorem.

The points do not have to be distinct. For example, if we have B'=A, then the result holds with the "chord" AB' being the tangent at A.
See The 3 Tangents and 3 Chords Theorem.

Tell me about Pascal