
Proof of the Dual Quadrilaterals Theorem
The Dual Quadrilaterals Theorem
If the quadrilateral ABCD is inscribed in a conic, and the
tangents at A,B,C,D (in order) define the circumscribed quadrilateral A'B'C'D',
then the diagonals of the quadrilaterals are concurrent.
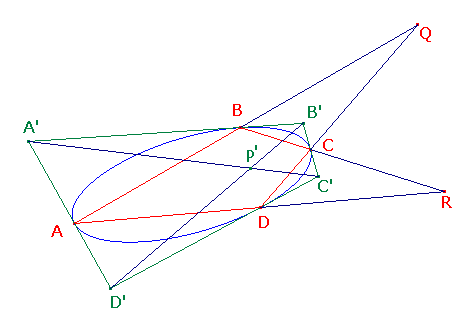
Proof
Let AB and CD meet in Q AD and BC in R, and B'C' and A'D' in P'.Observe that, since the tangents at B and C meet in B',
BC is the polar of B'.
Similarly, AD is the polar of D'.
By La Hire's Theorem, BC and AD meet in the pole of B'D'.
Thus R is the pole of B'D'.
Similarly, Q is the pole of A'C'.
Then, again by La Hire's Theorem, QR is the polar of P'.
But, by the Inscribed Quadrilateral Theorem,
the pole of QR is the intersection of AC and BD.
Thus the diagonals of the quadrilaterals are concurrent.