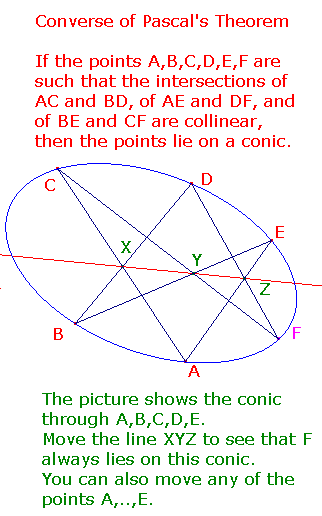
Pascal's Theorem states that if A,..,F lie on a conic, then X,Y and Z are collinear.

The converse is quite easy to deduce from the theorem.
Outline of a proof:
Consider the point F' where CY cuts the conic.
Apply Pascal's Theorem to A,B,C,D,E,F' to see that DF' must pass through Z (the intersection of AE and XY).
Then conclude that F=F'.

This allows us to obtain any number of points on the conic
defined by five fixed points A,B,C,D,E.

The Braikenridge-Maclaurin Construction
Let AC and BD meet in X.
Draw any line L through meeting BE and AE.
Suppose L cuts BE at Y and AE at Z.
Let CY and DZ meet at F.
By the Converse of Pascal's Theorem, F lies on the conic.

Of course the conic is the locus of points F so obtained.
The Cabri figure conpascal2.fig illustrates this.
If you don't have Cabri, there is a screen shot here.

Tell me about Pascal about Braikenridge about Maclaurin

Download conpascal.fig