

|
 The Inscribed Quadrilateral Theorem
The Inscribed Quadrilateral Theorem
If the vertices of a quadrialateral lie on a conic,
then the line joining the intersections of opposite sides
is the polar of the intersection of the diagonals.
Proof
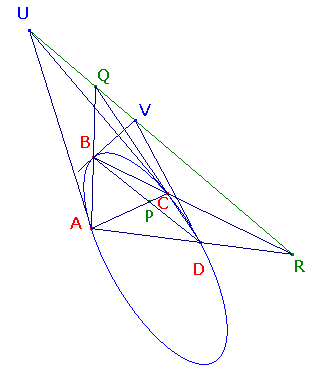
Let the tangents at A,C meet at U and those at B,D at V.
Apply Pascal's Theorem to the degenerate hexagon AABCCD.
The tangents from U meet the conic at A and C, so AC is the polar of U.
Suppose that the points A,B,C and D lie on the conic E,
that AC,BD meet at P, AB,CD at Q, and AD,BC at R.
We have to show that QR is the polar of P.
The "sides" AA and CC are the tangents at A and C respectively.
These meet at U, so that U,Q and are collinear.
Similarly, using the hexagon ABBCDD, V,Q and R are collinear.
Thus, U and V lie on QR.
Similarly, BD is the polar at V.
As AC and BD meet at P, P lies on both polars.
Then, by La Hire's Theorem, U and V lie on the polar of P.
Since U and V lie on QR, the result follows.
| Geometry Page |